zigzag писал(а): ↑2022-04-01 17:10:51
Так стало гораздое легче понимать.
А что такое tк?
А почему если в I2^2 tk*(1 - e-t/T) устремить T в бесконечность то получится I2^2 tk?
Я думал там типа I2^2 tk*(1 - e^0) = I2^2 tk*(1 - 1) = 0.
Действительно 0, ммм там дело в другом - изначально я по другому выводил, решил попроще объяснить, сам ошибся. Дело в следующем:
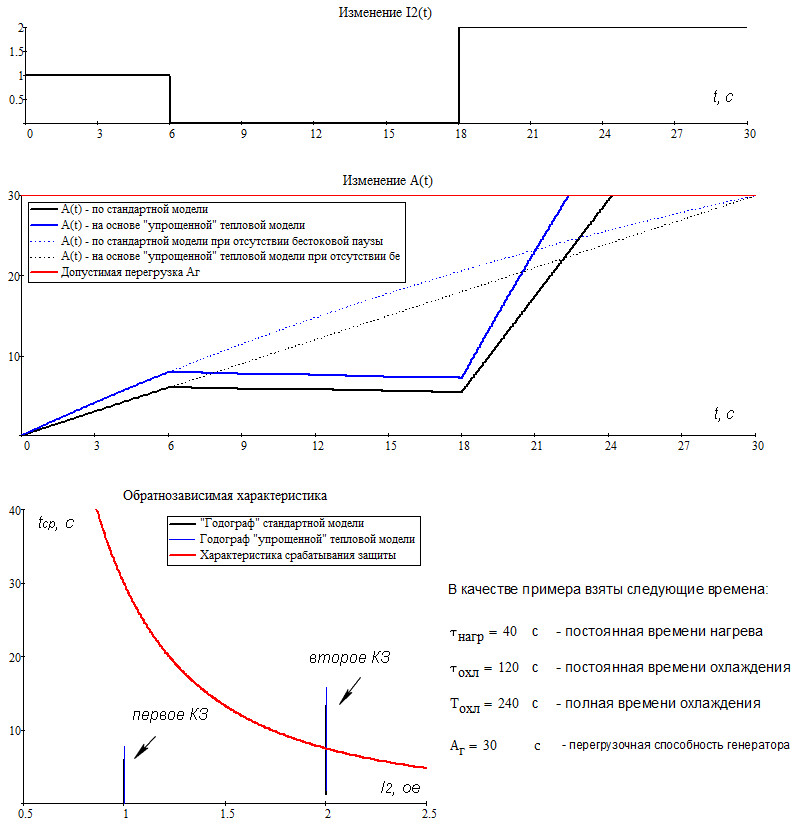
Стандартная модель при воздействии тока I2 = I2д = const будет увеличивать нагрев по линейному закону Арасч(t) = I2д^2*t, где I2д - ток обратной последовательности первый (хз как назвать, но надо понимать, что это не обязательно ток КЗ).
Упрощенная тепловая модель по закону Арасч_тм(t) = Ак*(1-e^-t/T), где Ак - "конечный" нагрев (аналог конечного превышения температуры). Этот нагрев мы можем представить как Ак = I2к^2*tк, где I2к - некий условный конечный ток (допустим не равный току I2д, поданному на стандартную модель, что вообще говоря только запутает, но мы же хотим показать почему I2 должно быть равно 1), а tк - некое конечное время.
Следовательно, стандартная и тепловая модели будут совпадать, если I2к^2*tк*(1-e^-t/T) = I2д^2*t. Откуда получим
tк = (I2д/I2к)^2*t/(1-e^-t/T) (1)
Уравнение (1) показывает чему необходимо принять tк для того, чтобы стандартная и тепловая модель совпали (или пока вернее сказать пересеклись) в момент времени t (или вернее сказать в точке {t, t}). Причем пока можно взять любые значения I2д, I2к и момент времени t0 (на графиках выше я взял момент t0 = Аг, I2д = 1, I2к = 1).
Теперь предположим, что на стандартную и тепловую модель подается ток КЗ равный I2 = I2д = I2к = I2кз, а tк мы вычисляли как tк = (I2д/I2к)^2*t0/(1-e^-t0/T). Подставив вычисленное значение tк в уравнение нагрева тепловой модели получим
Арасч_тм(t) = I2кз^2*tк*(1-e^-t/T) = (I2кз*I2д/I2к)^2*t0*(1-e^-t/T)/(1-e^-t0/T)
Устремив Т к бесконечности получим Арасч_тм(t) =(I2кз*I2д/I2к)^2*t, стандартная же модель даст Арасч(t) = I2кз^2*t, сравнивая реакцию моделей (выходные сигналы) видим, что для того, чтобы модели совпали (причем уже не только в точке t0) необходимо, чтобы I2д/I2к = 1, т.е. вместо частного условия I2к = I2д = 1 мы получили общее условие I2д/I2к = 1.
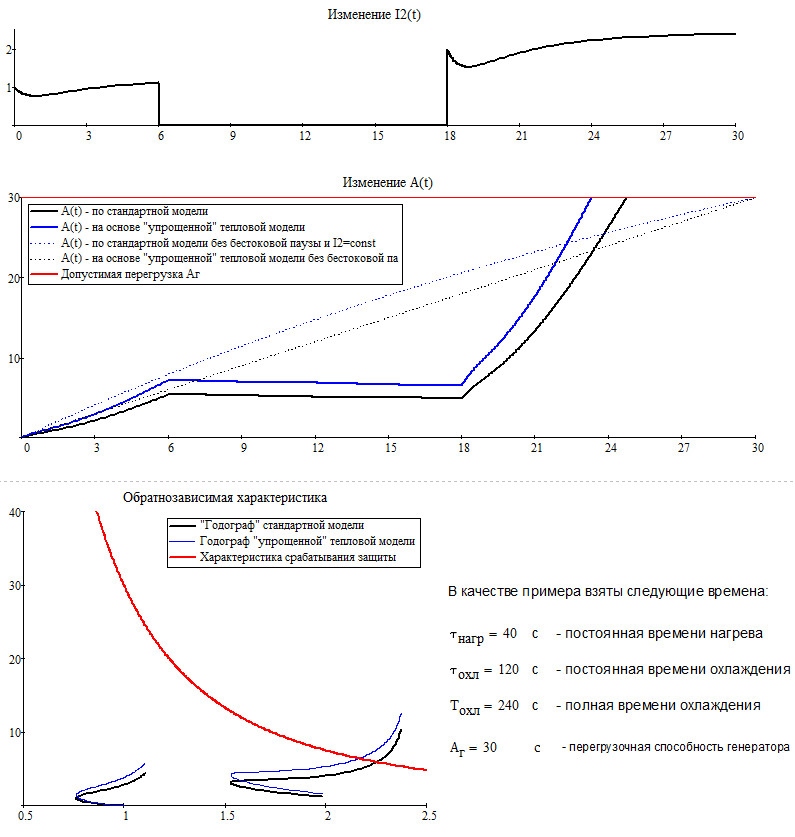
Вот как то так. И да подбором параметров можно добиться, чтобы решение тепловой модели пересекало стандартную модель не только в точке t = t0 = Аг с последующим приведением к стандартной модели устремляя Т к бесконечности, но и в других точках. Какая из моделей будет более близка к физике - надо проводить исследования (на первый взгляд кажется, что если t0 принимать Аг, то модель будет "нагреваться" не быстрее генератора).
Добавлено: 2022-04-04 13:10:09
hitakiry писал(а): ↑2022-04-01 14:26:08
Не любую. Надеюсь видео это покажет. Можно показать и аналитически, но всех секретов раскрывать не буду.
Выше речь шла про ток I2, а вы имели ввиду точку t0. Видимо не так Вас понял, поэтому написал, что не любую.