hitakiry писал(а): ↑2023-10-25 15:27:20
пока что это всего лишь ваши домыслы
Давайте даже без насыщения и индукции. Посчитаем переходной процесс в линейном ТТ с активной нагрузкой и отсутствии апериодики в первичном токе:
|----------------|--------------------|
| | |
ист. тока L R
| | |
|___________|_______________|
ток источника тока J = Im * sin(wt) - направлен вверх
ток в индуктивности i0 - направлен вниз
ток в резисторе i2 - направлен вниз
J = i0 + i2
L * di0/dt = i2 * R
Дифференциальное уравнение на i0
tau * di0/dt + i0 = Im * sin(wt)
tau = L/R
Ответ
i0 = R/Z*Im*sin(w*t - phi) + exp(-t/tau) * ( i0нач + R/Z*Im*sin(phi) )
i2 = X/Z*Im*sin(w*t - phi + pi/2) - exp(-t/tau) * ( i0нач + R/Z*Im*sin(phi) )
X = w*L
phi = arctg(X/R)
i0нач - начальное значение тока в индуктивности
Z = sqrt( R^2 + (wL)^2 )
Анализ:
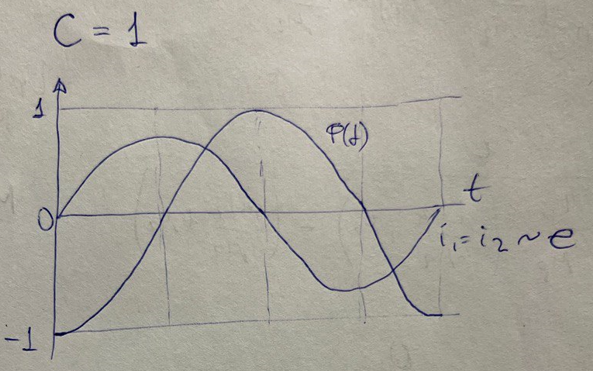
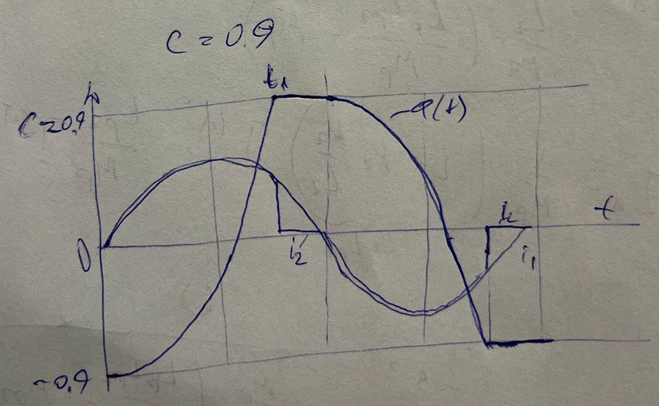
1. Апериодика есть как в токе намагничивания так и во вторичном токе: значит ТТ не в УР;
2. Апериодика затухнет через примерно 3*tau значит тогда примерно и наступит УР;
3. По мере роста L (приближаемся к ПХН) i2 стремится к i1, i0 стремится к нулю
4. Время наступления УР - 3*tau также растет по мере увеличения L так как tau прямо пропорционально L. То есть по мере приближения к ПХН начало УР неограниченно отдалятеся во времени.
Вы можете сказать что при L = бесконечность i0 = 0, i2 = i1 и формально мы в УР. Но по мне это выглядит странно так как получается весьма специфическая зависимость времени установления УР от L. Пока L - конечное число эти величины прямо пропорциональны, как только L = бесконечность то, время прыгает в ноль, то есть получается что предел
lim(k*L) при L стремящимся к бесконечности равен нулю.
А вот что по мне выглядит нормальным, так это задать i0нач таким чтобы i0 и i2 не содержали экспонент сразу с нулевого момента времени и независио от величины L, так как выбором i0нач можно занулить скобку у экспоненты. То есть в цепи сразу наступает УР. В этой задаче я подобрал нужное значение для i0нач. А в первоначальной задаче я выступал за то, чтобы в нужное значение устанавливать psi_нач. Идея остается без изменений.
Мне кажется именно такой УР имеют в виду авторы. Если вернуться к первоначальной задаче, то действительно разница во времени до насыщения только в первом периоде и я думаю, электромеханика не успеет почувстовать разницу.