Тема: Анимация метода симметричных составляющих
Коллеги, я выпустил новое видео, чтобы потомки отличали обратную последовательность от нулевой
https://youtu.be/hcPV1zI3_IY
|
Форум посвящен вопросам релейной защиты и автоматики (РЗА). Обмену опытом и общению релейщиков. |
Вы не вошли. Пожалуйста, войдите или зарегистрируйтесь.
Советы бывалого релейщика → Студенческий Раздел → Анимация метода симметричных составляющих

|
 |
Коллеги, я выпустил новое видео, чтобы потомки отличали обратную последовательность от нулевой
https://youtu.be/hcPV1zI3_IY
Спасибо. На днях провожу курсы, посвященные защитам ЭПЗ-1636, довольно актуально (один из компонентов - метод симметричных составляющих и его применение в соответствующей защите). Посмотрим, как мои слушатели оценят, по итогам выдам замечания (свои уже есть). Оно-то у меня есть и в "твердом" виде, причем хорошо наработано. Но в динамике пока не встречал.
Посмотрим, как мои слушатели оценят, по итогам выдам замечания (свои уже есть).
Замечания ОЧЕНЬ интересны. Очень жду!
Предварительно протестировал на своих студентах - слушателях. Уровень неслабый (от замначальника МСРЗАИ до представительницы ЦСРЗА, занимающейся, в основном, расчетами). Бегло посмотрели, мой вопрос "все поняли?". Ответы разной степени деликатности от "чего-то поняли" до "ниччегошеньки не поняли". Для меня-то это - очевидные вещи, хотя тоже не все понял и оценил. Время для знакомства с темой было крайне ограничено. Следующая встреча с ними предполагается во вторник - среду следующей недели. Хотел выдать в качестве раздатки (не у всех есть полноценный доступ к Интернету). Но скачать с первой попытки не сумел.
аналогично и на ютубе...
| Присоединяйтесь!!! Мы в социальных сетях и на Ютуб. |
Не воспринимает нормально мозг вращение векторов, которое не в плоски экрана происходит, а под углом к плоскости экрана. В зависимости от ракурса они и справа налево и слева направо и туда-сюда как качели вращаются. А вместе с вращающимися магнитами, тупить начинаешь, когда все вращается и качается и все в разные стороны.
Не воспринимает нормально мозг вращение векторов, которое не в плоски экрана происходит
А что такое "не в плоскости экрана"? У меня все в плоскости, кроме тех кадров, когда "зеркалю" обратную последовательность.
На мои видео нужно дисклеймер об эпилепсии ставить:)))
Таков уж метод симметричных составляющих...
В планах выпустить серию более простых видео, там не будет такого перебора.
А что такое "не в плоскости экрана"? У меня все в плоскости, .
Не утешайте себя. что у вас всё в плоскости.
Не всё! В плоскости экрана у вас вращаются магниты. Остальные стрелки, которые вращаются - вращаются под углом к плоскости экрана.
На снимке, для примера, белыми кружками выделил. Все вращающиеся стрелки рассеивают внимание и как следствие не можешь сосредоточиться на чем-то.
Дело ваше, но если хотите использовать как обучающий материал, лучше скорректировать.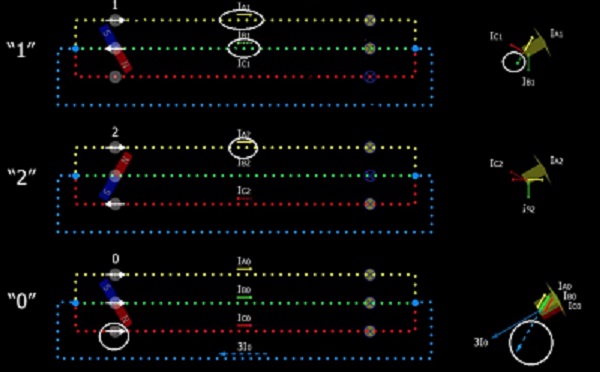 http://rzia.ru/uploads/images/8857/9e7ee731eea67322144d70fc99eebdb5.jpg
http://rzia.ru/uploads/images/8857/9e7ee731eea67322144d70fc99eebdb5.jpg
Не понял, что вы имеете ввиду. Где-то ошибка?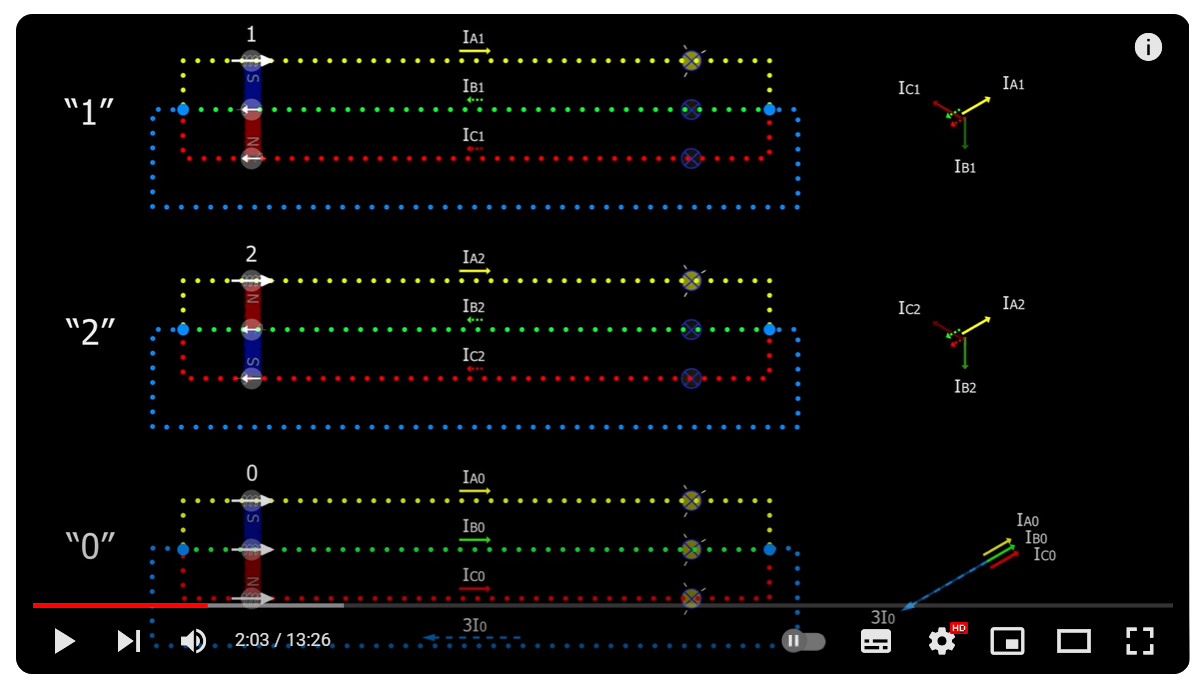 http://rzia.ru/uploads/images/22311/1bba55832c0b05086a231d399d4539bc.png
http://rzia.ru/uploads/images/22311/1bba55832c0b05086a231d399d4539bc.png
Не понял, что вы имеете ввиду. Где-то ошибка?
http://rzia.ru/uploads/images/22311/1bba55832c0b05086a231d399d4539bc.png
Ошибка в несоответствии информации воспроизводимой голосом за кадром той, что показана в мультфильме.
Что означают вращающиеся стрелки под наименованиями токов? Зачем эти стрелки вращаются разные стороны?
Зачем вращаются вектора электрических величин и в какую сторону они вращаются? Если они неподвижны, то что это меняет?
тупить начинаешь, когда все вращается и качается и все в разные стороны.
вот объяснение - "Таков уж метод симметричных составляющих..." а точнее такое его представление
автор считает, что если он понял так и, более того, показал, то это должно быть понятно и другим,
И что бы с моей стороны было всё понятно, то можно провести следующую аналогию - есть классическая мода и показ классических фасонов одежды просто появились новые ткани, технологии пошива и пр. - традиционное представление теории симметричных составляющих (вариации Эдванса), а есть типа высокая мода ради моды суперпуперновейшие дизайнерские решения... и если они кому-то не понравились , то это его проблемы... самое главное автору то понятно!!!
тоже не много туплю так как приходится постоянно тренировать воображение. ... всё просто представьте вместо вращения векторов движение синусоид и всё станет понятно ... их же значения действительно разные в различные моменты времени ... и максимум только у одной, а у другой минимум... и т.д. самое прикольное, что движение синусоид можно увидеть на аварийных осциллограммах и действительно сравнить предлагаемую торию с реальными переходными процессами, а вот получить такие картинки векторов в программах просмотра можно только после спец. обработки...
сразу предложил дополнить эту мультипликацию окнами с синусоидами
Эти стрелки не вращаются, а становятся то длиннее, то короче. Разъяснения я давал в своем базовом видео про трехфазку (на времени 1:06):
https://youtu.be/66zHTmLFH4I?t=66
Там же, кстати, привязка и к синусоиде идет.
Так я о том и говорю, то что Вы показали при объяснении в "базовом видео", нужно держать и представлять в голове при просмотре последнего, так сказать, ОБУЧАЮЩЕГО урока о симметричных составляющих!
получается ВЫ пытаетесь объяснить арифметические действия +/-, но для этого зачем-то используете собственные изображения чисел 1, 2, 3, ... N.
Эти стрелки не вращаются, а становятся то длиннее, то короче.
Вот оно как Вольдемар! Живу и не знаю, что изменение во времени направления наконечника на векторе с ← на → или наоборот это оказывается изменение длины! Герман Гроссман в восторг бы пришёл от такого применения векторов!
Коллеги, я выпустил новое видео, чтобы потомки отличали обратную последовательность от нулевой
Смотрел, смотрел, аж голова закружилась  :D
:D
И эмм... как бы повежливее, а на хрена, так сказать, козе баян?
В учебниках же всё есть. Зачем велосипед изобретаем, чтобы показать, что оно ещё и вращается (это ж очевидно)?
Вот отсюда должно получиться:
https://mega.nz/folder/W2gSEapC#vvI-RRfadJ-4fkUzePqLug
Для тех, кто совсем ничего не понял - рекомендую не сразу симметричные составляющие смотреть, а сначала ознакомиться с базовым видео про трехфазную систему (тоже можно скачать по ссылке).
У меня - можно оценить мгновенные значения составляющих друг относительно друга в любой момент времени .В учебниках такого не припомню (видел попытку изображения мгновенных величин для трехфазки, но не более того).
У меня - можно оценить мгновенные значения составляющих друг относительно друга в любой момент времени .В учебниках такого не припомню (видел попытку изображения мгновенных величин для трехфазки, но не более того).
Та ладно, посмотрите, например, Шнеерсона, там всё есть.
Вот собственно формулы, разве не красота?  ;) :
;) :
u1(wt) = 1/3·[ua(wt) + ub(wt+120°) + uc(wt-120°)]
u2(wt) = 1/3·[ua(wt) + ub(wt-120°) + uc(wt+120°)]
u0(wt) = 1/3·[ua(wt) + ub(wt) + uc(wt)]
Это не то же самое, на визуализацию эти формулы не претендуют.
У меня - можно оценить мгновенные значения составляющих друг относительно друга в любой момент времени .В учебниках такого не припомню
Согласен, мультипликационных учебников ещё не было, разве только "Вовка в тридевятом царстве", там вроде чертёж корыта есть, а потом волшебницы дворец рисуют, но это по деревообработке и строительству, а не электротехнике...
мгновенные значения наглядней наблюдать в динамике на синусоидах...
кстати, какой-то угол оси изменения векторов, а почему ось не строго горизонтальная или вертикальная? какой смысл?
мультипликационных учебников ещё не было, разве только "Вовка в тридевятом царстве"
А знаете есть ещё рисунки в движении с помощью перелистывания страниц. Мне нравится.
По сути анимация - это разновидость такого "динамического учебника". В этом смысле анимация действительно полезна.
Это не то же самое, на визуализацию эти формулы не претендуют.
Просто было заявлено, что в учебниках нет информации об оценке мгновенных значений симметричных составляющих (про визуализацию ничего не говорилось). Вот я и привёл формулы (которые позволяют это сделать). А теперь говорите про визуализацию. Я про неё ничего и не писал. Хотя и здесь я не вполне согласен: формулы прекрасно позволяют визуализировать мгновенные значения.
Предполагаю вы имели ввиду некую динамику: движение изображающей точки, вращение вектора и т.д. Тогда да, без анимации не обойтись.
Советы бывалого релейщика → Студенческий Раздел → Анимация метода симметричных составляющих
Форум работает на PunBB, при поддержке Informer Technologies, Inc
