Vorundnah писал(а): ↑2023-11-15 16:26:29
Вот этого не понял: вроде же любые три синусоидальные величины можно разложить на 1, 2 и 0? Имеется ли при этом связь между этими величинами (магнитная или какая-то еще) - не имеет принципиального значения для МСС.
Формулы МСС возникли именно из идеи развязывания магнитных связей.
Иначе этот МСС не особо нужен.
Ea---Za----|
Eb---Zb----|
Ec---Zc----|
Ia=Ea/Za
Ib=Eb/Zb
Ic=Ec/Zc
И тут любой вид КЗ считатется без проблем.
Реальная схема магнитосвязанная.
Обычно ее представляют вот так
Ea---ZL----|
Zm
Eb---ZL----|
Zm
Ec---ZL----|
(между сa тоже Zm)
Тогда логика примерно такая
Ea=ZL*Ia+Zm*Ib+Zm*Ic
Eb=Zm*Ia+ZL*Ib+Zm*Ic
Ec=Zm*Ia+Zm*Ib+ZL*Ic
[Ea] [ZL Zm Zm] [Ia]
[Eb] =[Zm ZL Zm] * [Ib]
[Ec] [Zm Zm ZL] [Ic]
Или
E=Z*I
Далее логика примерно такая
Представим уравнения вот так
[Ea] [ZL-Zm 0 0] [Ia] [Zm Zm Zm] [Ia]
[Eb] =[0 ZL-Zm 0] * [Ib] + [Zm Zm Zm] * [Ib]
[Ec] [0 0 ZL-Zm] [Ic] [Zm Zm Zm] [Ic]
Падение напряжения на второй части уравнения запишется так
dUa=Zm*Ia+Zm*Ib+Zm*Ic=Zm*(Ia+Ib+Ic)
dUb=Zm*Ia+Zm*Ib+Zm*Ic=Zm*(Ia+Ib+Ic)
dUc=Zm*Ia+Zm*Ib+Zm*Ic=Zm*(Ia+Ib+Ic)
Т.е. можно магнитные связи трех фаз заменить одним нулевым проводом вот так
Ea---ZL-Zm----|
Eb---ZL-Zm----|---Zm---*
Ec---ZL-Zm----|
И далее логика такая.
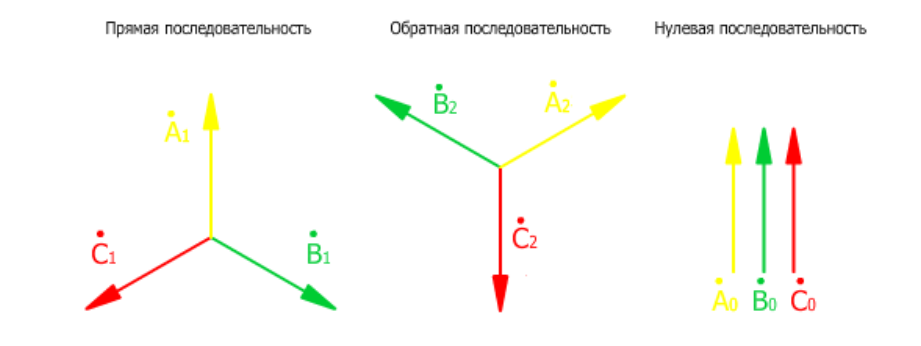
Подаем прямую и обратную последовательность.
Математически - в общем случае - 2 такие разные трехфазные группы токов, чтобы они не создавали тока через нулевой провод.
В нулевом проводе, очевидно, ток не течет, Z1=Z2=ZL-Zm
Т.е. для прямой и обратной последовательности нулевой провод можно закоротить. Т.к. фазы симметричные, то можно взять всего одну.
Подаем нулевую последовательность.
В общем случае математически надо подать такие токи в фазах, чтобы попарная их разность была нулевой, (потому что все, что не течет через нулевой провод, выражено через I1 и I2). Отсюда получается надо подать 3 одинаковых тока в фазах.
Ea=(ZL-Zm)*I+Zm*3I=(ZL+2*Zm)*I
Сопротивление нулевой последовательности ZL+2*Zm
Далее - почему собственно последовательностей, исключая нулевую, ровно 2? Потому что если ток не течет через нулевой провод, то ток третьей фазы выражается через 2 других. Итого у нас при отсутствии тока через НП у нас 2 независимых тока, и мы их выражаем через 2 последовательности (т.е. 2 независимых переменных было и 2 осталось).
...
для чего это все нужно.
Реальная схема это здоровая сеть, и в начале 20 века, когда не было компьютеров, считали все руками или на расчетных столах (соединяли на стенде резисторы проводами и меряли напряжения токи). И если задаться вопросом - а как свернуть до 1 сопротивления 1 ЭДС, например, чтобы посчитать ТКЗ в месте повреждения - то в общем случае нужно будет возводить матрицы 3х3 в минус первую степень, например, для запараллеливания Zэкв=(Z1^-1+Z2^-1)^-1
И в начале 20 века это занятие было слишком мутным для инженеров. И метод симметричных составляющих (и аналогичные ему по логике действия dq0 преобразование, альфа-бета-0 преобразование, правда они немного для другого) были придуманы для того, чтобы развязать взаимоиндукции.
Тогда можно схемы прямой, обратной, нулевой последовательности сворачивать руками, как однолинейные, т.к. между ними нет магнитных связей. И остается только вопрос несимметрии в точке КЗ, который решается через граничные условия, например.
И на расчетных столах также можно будет собрать схему в последовательностях, их как-то соединить (в зависимости от вида КЗ), померить напряжения и токи в последовательностях, а потом пересчитать в фазные напряжения и токи.
Т.е. математически как бы часть работы по возведению в -1 степень матриц (и в общем случае - взятия некоторой функции от матрицы) - через разложение на симметричные составляющие выполняется аналитически, и остается доделать руками.
Ограничение - нужна идеальная симметрия, т.е. все фазы сопротивление ZL, взаимоиндукции Zm (в общем случае они разделяются на 2 группы Zm1, Zm2). Если сделать сопротивления фаз и взаимоиндукций разными (как это по физике и есть), то на самом деле полного развязывания магнитных связей не произойдет, и, если этим пренебречь и считать, что Z0, Z1, Z2 не взаимоиндуктируют между собой - будет некоторая расчетная погрешность. Но этим обычно пренебрегают.