Я хотел бы сказать пару слов о том какой алгоритм хуже/лучше в плане оценки частоты. Кто-то за переходы через ноль, кто-то за производную фазы (а алгоритмов не 2 и не 3). Но в словесных переписках вряд ли что-то можно доказать, потому что у оппонента всегда есть козырь «а у меня вообще еще фильтр стоит», «а некратных гармоник такой амплитуды не бывает» и так далее.
Чтобы сравнить надо поставить алгоритмы в одинаковые условия (дать им одинаковое количество информации) и сделать набор тестов с одинаковыми критериями оценки.
Я сделал один тест из множества возможных для пары «переходы через ноль» vs «производная фазы» в плане реакции на небольшой шум. Обращу внимание что мы смотрим не на абсолютные величины погрешностей, а на соотношение между двумя алгоритмами.
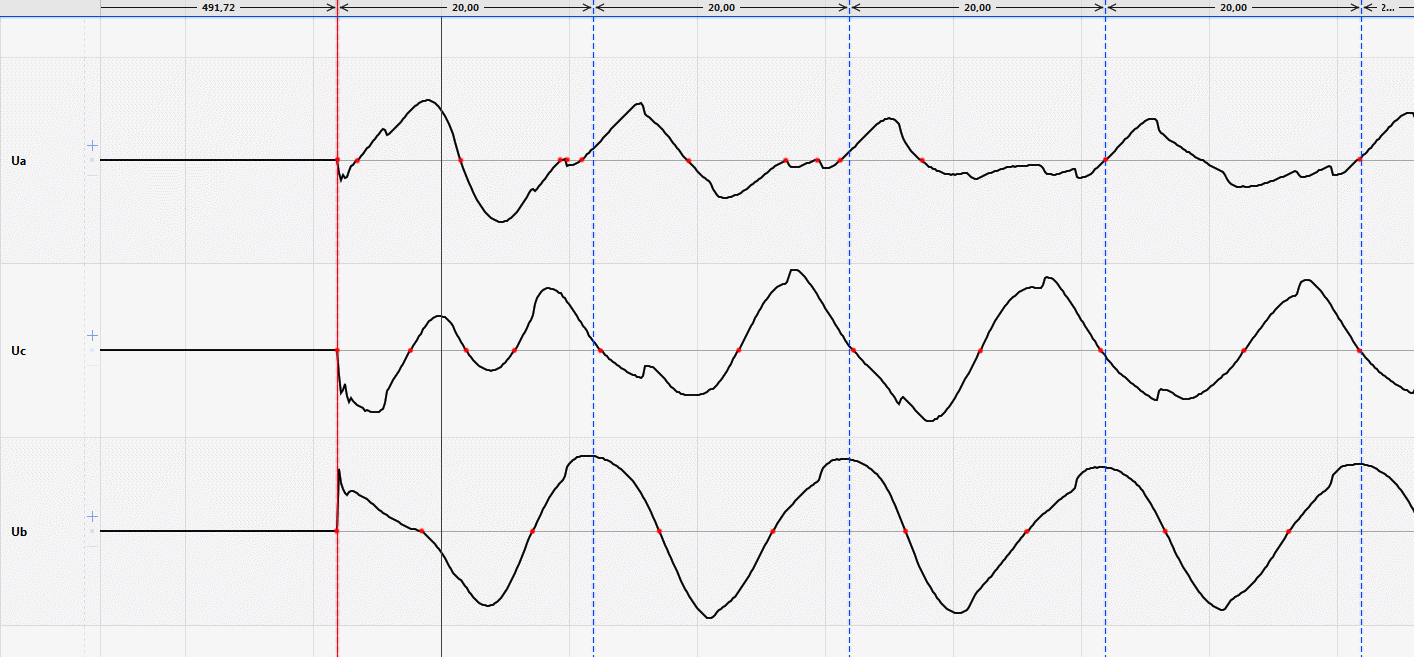
Исходный сигнал это синус частоты 50 Гц с начальной фазой, равномерно распределенной в пределах плюс минус половина периода дискретизации (чтобы переход через ноль случайно попадал на период дискретизации) плюс белый шум с равномерным распределением (такой как раз от АЦП) величиной 1%, 40 точек на период.
 http://rzia.ru/uploads/images/15941/3b69f875305927fe2aed88bdd86c339f.png
http://rzia.ru/uploads/images/15941/3b69f875305927fe2aed88bdd86c339f.png
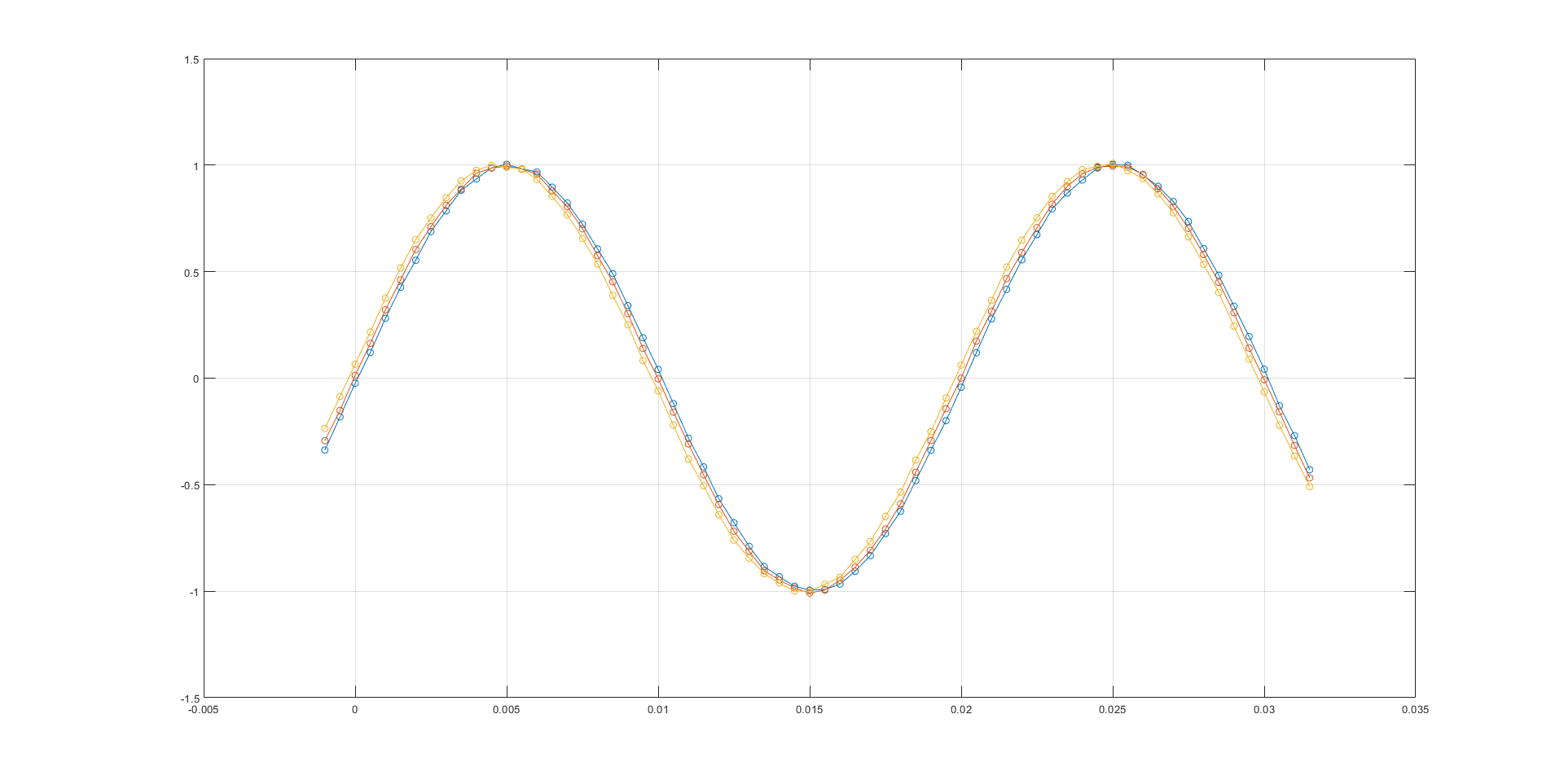
На таком сигнале есть два перехода из плюс в минус и два из минуса в плюс. Можно посчитать длины двух периодов (момент перехода с помощью линейной интерполяции) и усреднить. Предфильтрация невозможна так как часть точек придется отдать чтобы заполнить линию задержки фильтра. Количество отфильтрованных точек (после окончания переходного процесса в фильтре) будет меньшим и у нас не будет 4-х достоверных переходов через ноль. Плюс к этому предфильтрацию можно применить как до применения одного алгоритма, так и до применения другого, что в теории не даст хоть одному преимущество.
На этом же сигнале считается Фурье и по полученным векторам определяется скорость изменения их фазы. В теории она меняться не должна, так как сигнал 50 Гц, но из-за шума будут колебания.
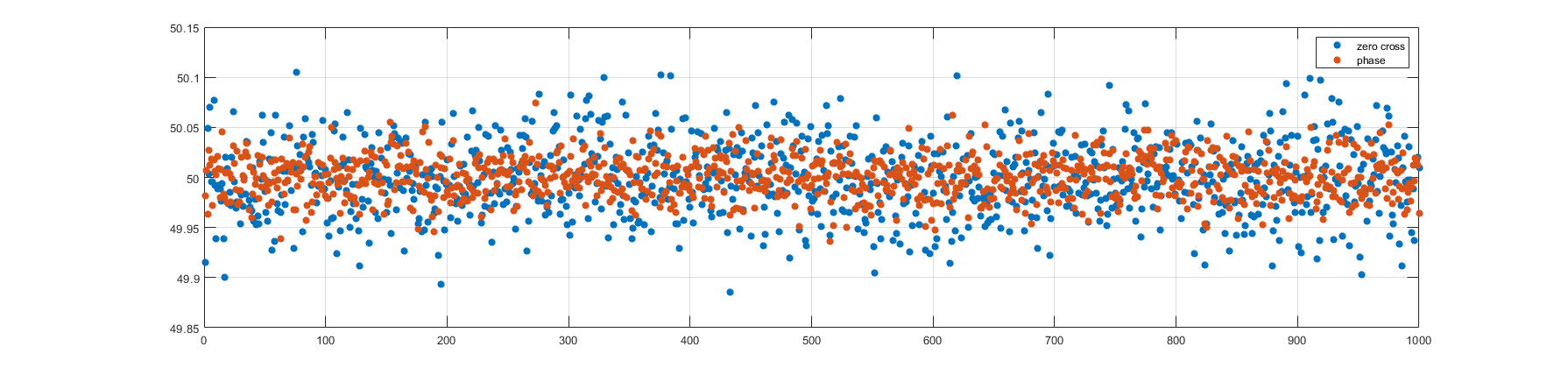
В итоге по этому сигналу можно получить одно значение частоты как одним, так и другим алгоритмом. Повторяем эту процедуру 1000 раз (чтобы шум был всегда разным) и получаем следующие картины.
 http://rzia.ru/uploads/images/15941/5940cd1eb61ea1d5633fb3da8c63fca5.png
http://rzia.ru/uploads/images/15941/5940cd1eb61ea1d5633fb3da8c63fca5.png 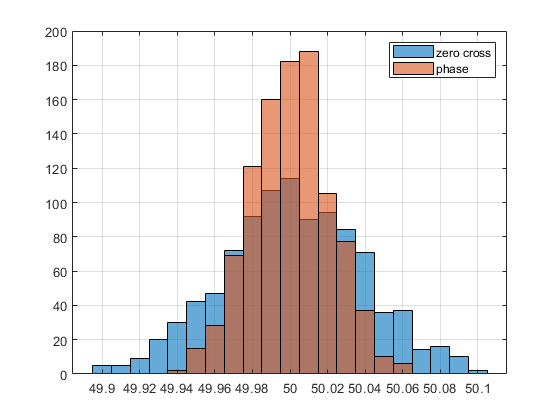 http://rzia.ru/uploads/images/15941/482d4020165a67f15e5a2f80eca7b92b.png
http://rzia.ru/uploads/images/15941/482d4020165a67f15e5a2f80eca7b92b.png
Из графиков видно, что способ по фазе работает с меньшим разбросом, следовательно в этом тесте он справился лучше.
Такие графики на мой взгляд есть результат самого большого ограничения алгоритма по переходу через ноль – то, что информация о частоте берется из малого количества точек около нуля, которые к тому же больше всего подвержены шуму квантования. Алгоритм по производной фазы же использует информацию из всех точек и поэтому с шумом справляется лучше.
При увеличении частоты дискретизации равновесие смещается еще больше в сторону алгоритма по производной фазы, так как коэффициенты Фурье начинают «шуметь» еще меньше (шум уменьшается как 1 / sqrt( кол-во точек на периоде ) ).
Как можно улучшить алгоритм перехода через ноль? Например, фиксировать переходы не только через ноль, но и через 1В, 2В, -1В, -2В и так далее. Таким образом мы за тоже время получим больше длин периодов, а значит шум снизится. Но так вряд ли кто делает, так как эти уровни должны как-то учитывать реальную амплитуду сигнала.
Считать время перехода с помощью кубической интерполяции (по четырем точкам), думаю, бессмысленно, так как точки зашумлены и нет смысла строить кривую, которая пройдет через все зашумленные точки.
А вот МНК как раз тут подходит. Будем считать время перехода через ноль, проводя прямую с помощью МНК через 4 точки (2 выше нуля и 2 ниже). Получим следующий результат.
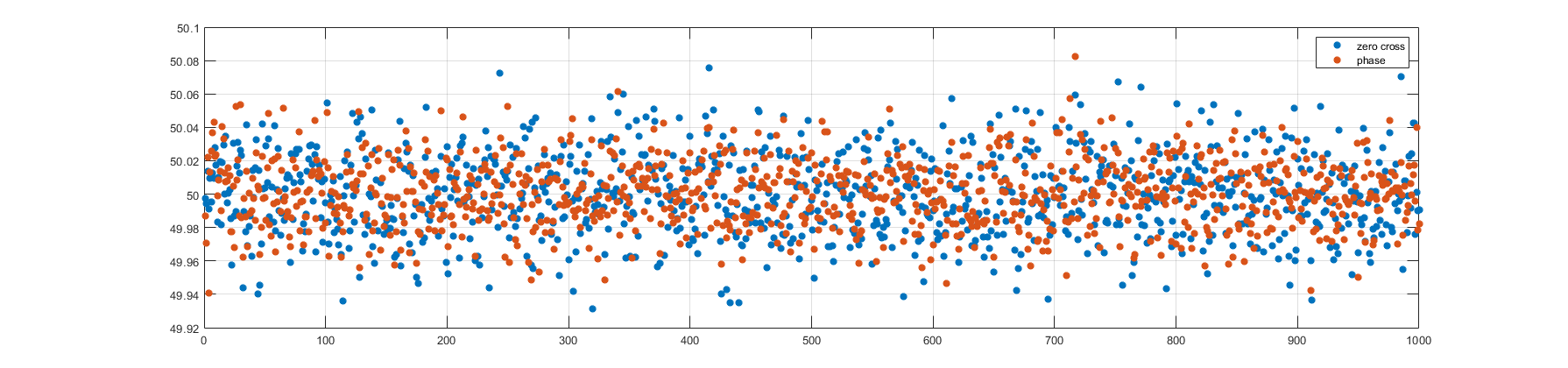 http://rzia.ru/uploads/images/15941/6285ae9f80387bbcc3ddea307d8a40a2.png
http://rzia.ru/uploads/images/15941/6285ae9f80387bbcc3ddea307d8a40a2.png 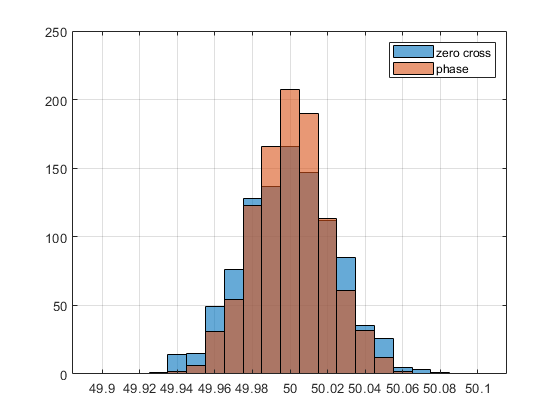 http://rzia.ru/uploads/images/15941/edb355823fb62a423d112bfc9db40128.png
http://rzia.ru/uploads/images/15941/edb355823fb62a423d112bfc9db40128.png
Действительно гораздо лучше, потому что теперь в расчете частоты используется больше точек сигнала. Но все равно чуть хуже, чем по производной фазы.
Справедливости ради при изменении частоты на 55 Гц, алгоритм по производной фазы (в конкретно этой реализации) дает методическую погрешность так как расчет производной уже не так хорошо борется с двойной частотой (50 + 55 = 105 Гц). Но это уже другой тест.
Добавлено: 2022-02-22 14:23:38
ПАУтина писал(а): ↑2022-02-22 13:44:16
Например. 2 сигнала близких частот 49Гц и 51 Гц и близких по амплитуде и дали только окно когда они начинаются в противофазе и длительность окна только 30...40 мс - сигнала может вообще не наблюдаться - это Вам не гашение нуля гармониками, когда амплитуды всё равно растут или по крайней мере не уменьшаются. Можно восстановить только методом перебора ... а вот если окно будет 1/(51-49) = 0,5 c, то можно сразу даже просто на глаз сказать, что это и какое гармоники.
Параметрические методы оценки спектра позволяют различать близкие частоты за гораздое меньшее временное окно.
Добавлено: 2022-02-22 14:25:59
retriever писал(а): ↑2022-02-22 12:38:08
Если сигнал именно периодический, то, наверное, можно попытаться пошаманить с автокорелляцией
A New Method for Fast Frequency Measurement for Protection Applications B. Kasztenny
Schweitzer Engineering Laboratories, Inc
Если вдруг не видели.