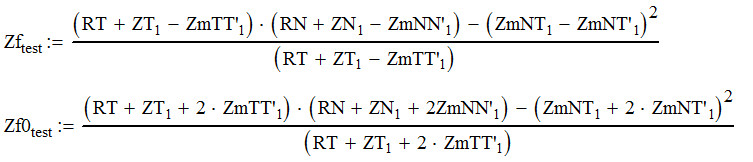retriever писал(а): ↑2023-01-16 19:12:06
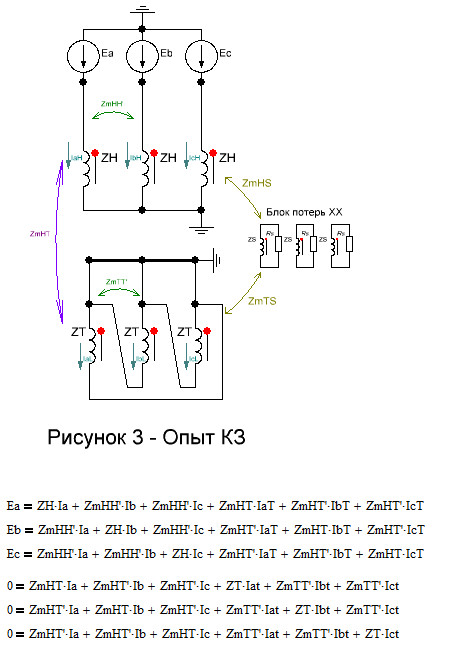
Когда на стороне треугольника 3ф КЗ, то треугольник фактически исчезает и остаются только три короткозамкнутые отдельные обмотки.
понял - эти уравнения справедливы и для трансформатора Yn/Y и для Yn/D. Да и вообще тут группа соединения трансформатора ни при чем, т.е. даже если обмотки не соединять в группу уравнения все равно будут справедливы.
Внимательно проанализировал Ваш вывод и пришел к выводу, что сопротивления прямой и нулевой последовательности трансформатора можно записать в том виде как у Вас (обозначения взял по Ченю), т.е.
z1 = (zp - z'm) - (zm - z''m)^2/(zs - z'''m) (1)
z0 = (zp + 2·z'm) - (zm + 2·z''m)^2/(zs + 2·z'''m) (2)
а можно представить в другом виде:
z1 = z1сигма + z2сигма II (zm - z''m) (3)
z0 = z1сигма0 + z2сигма0 II (zm + 2·z''m) (4)
P.S.: Все сопротивления пока приведены к одному напряжению.
Так вот, если принять, что
zm = (Zp - Zхх) + Dхх
при этом
z1сигма = z2сигма = Zальфа + (Zальфа^2 + Zкз*Dхх)^0.5, где Dхх = (Zхх*(Zхх - Zкз))^0,5
z1сигма0 = z2сигма0 = Zхх - Dхх Zальфа = Zкз/2 - Dхх
получим, что z1сигма = z1сигма0, и z0/z1 = k
Если же принять
zm = (Zp - Zхх) - Dхх, то
z1сигма = z2сигма = Zбета - (Zбета - Zкз*Dхх)^0.5, где Dхх = (Zхх*(Zхх - Zкз))^0,5
z1сигма0 = z2сигма0 = Zт0·(Dхх - Zт0 + Zхх) / (2Dхх - Zт0 + 2 Zхх) Zбета = Zкз/2 + Dхх
то получим z1сигма0/z1сигма примерно равно k, а отношение Zт0/Zт также равно k
т.е. получается, что для того, чтобы Zт0/Zт = k сопротивление рассеяния zсигма может быть как равно zсигма0, так и не равно zсигма0 (т.е. возможно два варианта, в зависимости от того, чему принимается Zm). Соответственно, если zсигма = zсигма0, то формула Щедрина полностью справедлива, даже в случае Zт0/Zт = k.
Кстати сопротивления рассеяния трансформатора можно также определить и по другим формулам (правда если известны входящие параметры):
Z1сигма = (Zp - Z'm) - (Zm - Z''m)
Z2сигма = (Zs - Z'''m) - (Zm - Z''m)
Z1сигма0 = (Zp + 2Z'm) - (Zm + 2Z''m)
Z2сигма0 = (Zs + 2Z'''m) - (Zm + 2Z''m)
Откуда с учетом (1) и (2) можно легко вывести формулы (3) и (4).