Re: Определение частоты сигнала
Метод хороший в диапазоне частот 40-60 Гц при условии что еще применена фильтрация выходного сигнала фильтра Фурье на интервале 20мс...
|
Форум посвящен вопросам релейной защиты и автоматики (РЗА). Обмену опытом и общению релейщиков. |
Вы не вошли. Пожалуйста, войдите или зарегистрируйтесь.
Советы бывалого релейщика → Как проводить анализ осциллограмм аварийных регистраторов → Определение частоты сигнала

|
 |
Метод хороший в диапазоне частот 40-60 Гц при условии что еще применена фильтрация выходного сигнала фильтра Фурье на интервале 20мс...
Если я правильно понял, то для такого метода нужно окно наблюдения в два периода минимально возможной частоты - один, чтобы получить первое значение, и еще один, чтобы накопить значения, на которых считать дисперсию?
Да, примерно так. На окне наблюдения делал ресемплинг, чтобы фильтр Фурье работал с тем окном, которое надо (условно, 1/50=0.02 с для 50 Гц и 1/51=0.019608
для 51 Гц).
Ресемплинг можно делать кусочно-линейный (это самый быстрый), либо можно заморочиться с монотонными сплайнами.
Я брал реальные осциллограммы с КЗ и строил для них частоту от времени. В осциллограммах была какая-то апериодика у токов, какие-то небольшие махры в напряжениях... более-менее нормально определялась частота 50 Гц +- какие-то мелкие дроби (что-нибудь типа 49.95 Гц).
По напряжениям частота хорошо считалась (особенно если обработать данные по всем трем фазам). По токам хуже (апериодика мешала и всякие искажения синусоиды токов).
Вот
comtradematlabparserv091.zip
Запускать TEST_OSCILL_HANDLE.m
(также можно прочесть комтрейд файлом TEST_READ_COMTRADE и записать что-то в комтрейд файлом TEST_WRITE_COMTRADE)
А что если увеличить количество выборок? Часть точек - это пересечение с нулём, а часть это экстремумы (когда производная меняет знак).
Неа.
Я делал такую штуку, окно 0.04 с
1 период (0.02 с) Фурье-фильтр и далее накапливаются значения еще за 0.02 с результаты фильтрации, по ним берется дисперсия.
Мне кажется идейно это похоже на ФАПЧ. И там и тут нужно так подстроить частоту фильтра Фурье и период интегрирования чтобы вектор остановился (равно дисперсия стала минимальной). В ФАПЧ это делается в контуре обратной связи по разностной частоте, а тут в лоб вычисляется подбором нужной частоты (или более быстрым методом). Вычислений, конечно, много (если правильно понял). Надо посчитать Фурье на каждой точке да еще и несколько раз, пока процесс не сойдется. Не все современные терминалы всё успевают посчитать даже один раз между соседними точками, поэтому переходят на расчеты раз в 2.5, 5, 10 мс.
А можно чуть подробнее по алгоритму? Ищем абсциссу минимума функции D(f)? Эта функция примерно похожа на параболу? Получается что при идеальных сигналах и идеальной настройке и дисперсия и производная дисперсии равны нулю, что приводит к соотношению 0/0 в выражении для обновления f.
Добавлено: 2021-03-31 21:55:14
А какие?
Получается что при идеальных сигналах и идеальной настройке и дисперсия и производная дисперсии равны нулю, что приводит к соотношению 0/0 в выражении для обновления f
Да, наверное, нужно добавить условия, что если на первом шаге дисперсия ноль (ровно 50 Гц), то поиск прекратить. И что если во время обновления дисперсия стала где-то ноль или тем более производная от нее ноль, то поиск остановить на требуемом значении.
А так будет какое-то колебание, скорее всего. Дисперсия D(f) и D(f+df) обычно всегда разные (хотя может быть по математике есть какие-то странные случаи, когда они совпадают). Тогда по Ньютону мы попадаем в новое значение f, не такое, какое было, и получаем новое значение df, и будет в итоге значение частоты, близкое к настоящему, но не равное ему.
Не помню уже, это было 2-3 года назад. Но это были методы из гугловыдачи.
Какие-то разрекламированные методы. Вроде бы даже из книжки Phadke, Thorp (но это неточно).
| Присоединяйтесь!!! Мы в социальных сетях и на Ютуб. |
Да, наверное, нужно добавить условия, что если на первом шаге дисперсия ноль (ровно 50 Гц), то поиск прекратить. И что если во время обновления дисперсия стала где-то ноль или тем более производная от нее ноль, то поиск остановить на требуемом значении.
Мне кажется несоответствие немного другое.
Процесс вида:
x(n) = x(n-1) - f ( x(n-1) ) / f' ( x(n-1) )
ищет не минимум функции f(x), а ноль (корень). И это логично, сама функция стремится к нулю, а производная нет и на каждом шаге добавка всё уменьшается и уменьшается. А в районе минимума функции данный процесс может начать колебания рядом с минимумом.
Для поиска минимума функции f(x) ищут корень функции f'(x), значит процесс для поиска минимума функции дисперсии должен выглядеть как
x(n) = x(n-1) - f' ( x(n-1) ) / f'' ( x(n-1) )
Пользователь писал(а): ↑
Вчера 15:13:31требование 0,02 Гц за 0,06 сек - должно выполняться
только при отношении сигнал/шум > какой то величиныОно должно выполняться во всех режимах,
Это физически невозможно,
x(n) = x(n-1) - f ( x(n-1) ) / f' ( x(n-1) )
ищет не минимум функции f(x), а ноль (корень). И это логично, сама функция стремится к нулю, а производная нет и на каждом шаге добавка всё уменьшается и уменьшается. А в районе минимума функции данный процесс может начать колебания рядом с минимумом.
Дисперсия сигнала D(f) есть функция от f
мы фильтруем массив значений сигнала x фильтром Ф(f) несколько раз,
получаем набор отфильтрованных отсчетов Xdft(f)=filter(x,f)
далее находим дисперсию D(x_all, f)=D(filter(x1,f)...filter(x2,f)....filter(xn,f)), x_all=[x1,x2....xn], сами x1,x2... это тоже массивы, выделяемые из окна данных, со сдвигом.
Далее нам надо подобрать такую частоту f, чтобы D(x_all,f) была равна нулю, т.е. получается уравнение D(f)=0.
f получается корень. df на каждой итерации по Ньютону уменьшается, поэтому, если все правильно сделать, колебаний быть не должно (разве что какие-то мелкие, из-за округления).
Зачем там минимум и вторая производная? Тем более, что все равно численно производную придется искать.
Да, но дисперсия функция неотрицательная по определению. И в лучшем случае равна нулю, когда весь массив идентичен. Значит эта функция по виду некая парабола, которая в лучшем случае касается оси абсцисс в своем минимуме, а на самом деле наверняка чуть выше. И итерационный процесс для нахождения корня может, например, сделать следующее:
https://ru.wikipedia.org/wiki/%D0%A4%D0 … on_bad.PNG
Искать вторую производную численно, конечно, не стоит. Но если всё-таки искать точку минимума то можно просто взять другой численных алгоритм типа золотого сечения.
Да, но дисперсия функция неотрицательная по определению. И в лучшем случае равна нулю, когда весь массив идентичен.
А, понял.
Да, наверное так лучше.
Добавлено: 2021-04-01 12:49:02
Или действительно попробовать другие способы поиска минимума.
Почему Вы так считаете?
Получается все сертифицированные по этому стандарту обманули СО ЕЭС?
Почему Вы так считаете?
Получается все сертифицированные по этому стандарту обманули СО ЕЭС?
ОК,
Вы знаете условия, при которых проводят сертификацию ?,
в них и должно быть задано отношение сигнал/шум
В СТО 59012820.29.020.003-2016 описаны в том числе и сертификационные испытания.
Ни в самих требованиях к АЧР, ни в испытаниях ничего про соотношение сигнал/шум не написано.
Потому что это не академическая задача, и тут никого не интересует точность измерения каких-то абстрактных сигналов с каким-то соотношением сигнал/шум.
Задача - чтобы в тех режимах, в которых может оказаться АЧР, устройство всегда работало правильно. В одних режимах это обеспечивается точность измерения, в других - например, блокировкой по скорости изменения частоты или по минимальной рабочей частоте.
Задача разработчика - чтобы во всех режимах, когда измерение частоты требуется, оно было достаточно точным.
Смысл в том, что у нас не америка и вместо 50 Гц не может оказаться 60 Гц или там 30 Гц или сигнал с какими-то очень мощными ВЧ-всплесками. Там везде синусоида примерно 50 Гц частотой, не очень загрязненная, для нее вполне реально сделать определение частоты за малый промежуток времени.
Если бы у нас был какой-то радиосигнал, где есть куча разных частот, тогда да, надо было бы брать большое окно данных.
"На Ваш запрос сообщаем, что шкафы РЗА серий П1Э2607, ШЭ2710 производства ООО НПП «ЭКРА» не имеют ограничений в работе при частоте электрического тока в диапазоне от 45 Гц до 55 Гц."
ВЧ связь, Uвч~100В
рядом СВ станция, мощности порядка киловатта, напряжения сотни вольт наводки
----------
что такое сигнал/шум: разместите в комнате "Академический ансамбль песни и пляски Российской армии", и попробуйте поговорить,
так что - "не академическая задача, и тут никого не интересует точность измерения"
Я потестил этот алгоритм, который выше. Там есть определенные затыки с Ньютоном, т.е. всякие кривые значения, которые иногда он выдает, связаны с кривизной алгоритма поиска минимума дисперсии (точка минимума пролетает, и далее начинаются кривые итерации "не туда").
Но для контроля сделал поиск минимума по методу золотого сечения. Работает хорошо (брал сигнал с рандомным шумом в несколько процентов). Но долго. Надо еще думать над производительностью и тестировать.
ВЧ-сигналы подавляются Фурье-фильтром почти полностью. Все, что порядка килогерца и выше - должно давиться почти в ноль.
Если взять среднее значение от массива F в листинге то это и будет примерное значение частоты сигнала (особенно если длина массива будет кратна 10 мс). Это значение и можно брать для очередного пересчёта Фурье. А останавливать либо по минимуму дисперсии либо по малому изменению в частоте от расчета к расчёту.
Дисперсия сигнала D(f) есть функция от f
мы фильтруем массив значений сигнала x фильтром Ф(f) несколько раз,
получаем набор отфильтрованных отсчетов Xdft(f)=filter(x,f)
далее находим дисперсию D(x_all, f)=D(filter(x1,f)...filter(x2,f)....filter(xn,f)), x_all=[x1,x2....xn], сами x1,x2... это тоже массивы, выделяемые из окна данных, со сдвигом.Далее нам надо подобрать такую частоту f, чтобы D(x_all,f) была равна нулю, т.е. получается уравнение D(f)=0.
f получается корень. df на каждой итерации по Ньютону уменьшается, поэтому, если все правильно сделать, колебаний быть не должно (разве что какие-то мелкие, из-за округления).Зачем там минимум и вторая производная? Тем более, что все равно численно производную придется искать.
Я так понимаю, весь смысл всех этих математических "изощрений" заключается в том, что если нельзя просто определить частоту сигнала как число колебаний в единицу времени путём измерения периода (или полупериода), то вычисление частоты производится путём перебора или подстановки значений частоты, пока на и большим образом не будет удовлетворять точности. Действительно, если частота синусоиды 50 Гц и взяли это значение, то дисперсия будет ноль, более того если она скажем 49,97747812731 и взять такую же, то будет также...
Где-то ещё лет 25 назад таким способом вычислял частоты двух эквивалентных эдс при АР, путём точного измерения периода АР, всё было замечательно если он был постоянным, но как только брал натурные сигналы АР, всё разваливалось, поэтому и забросил (да и компьютера не было хорошего, считал на MatchCad 2.0 ещё под DOS на Мозовия с тактовой 2,38 МГц - один опыт считался 3...4 мин.).
В общем, еще раз покрутил алгоритм ради интереса. Сделал 2 метода - с поиском минимума по золотому сечению, и метод, который вначале ищет Ньютоном, потом - по золотому сечению.
На домашнем компе (Core i9) все летает довольно быстро, но так скорость может быть не очень большой.
comtradematlabparserv092.zip
Вот картинки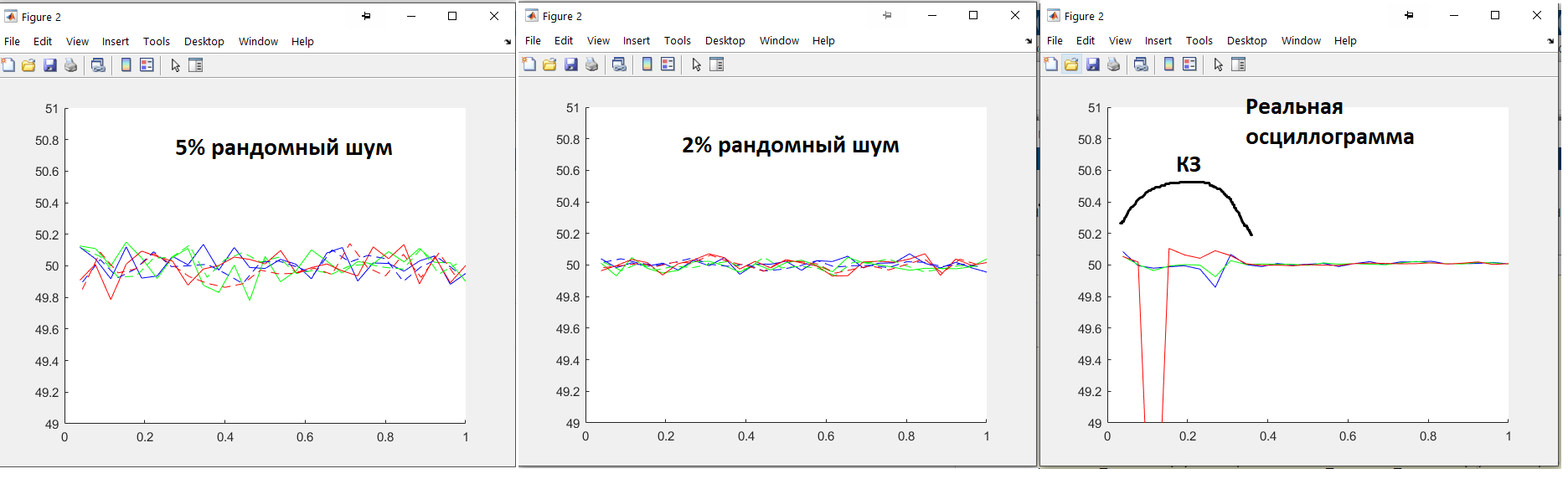 http://rzia.ru/uploads/images/4731/36b223b760b524806ffbcb2bb33aa5cc.png
http://rzia.ru/uploads/images/4731/36b223b760b524806ffbcb2bb33aa5cc.png
Вот картинки
http://rzia.ru/uploads/images/4731/36b223b760b524806ffbcb2bb33aa5cc.png
требование 0,02 Гц за 0,06 сек
у вас сколько ошибка получается?
Советы бывалого релейщика → Как проводить анализ осциллограмм аварийных регистраторов → Определение частоты сигнала
Форум работает на PunBB, при поддержке Informer Technologies, Inc
