Re: Анимация метода симметричных составляющих
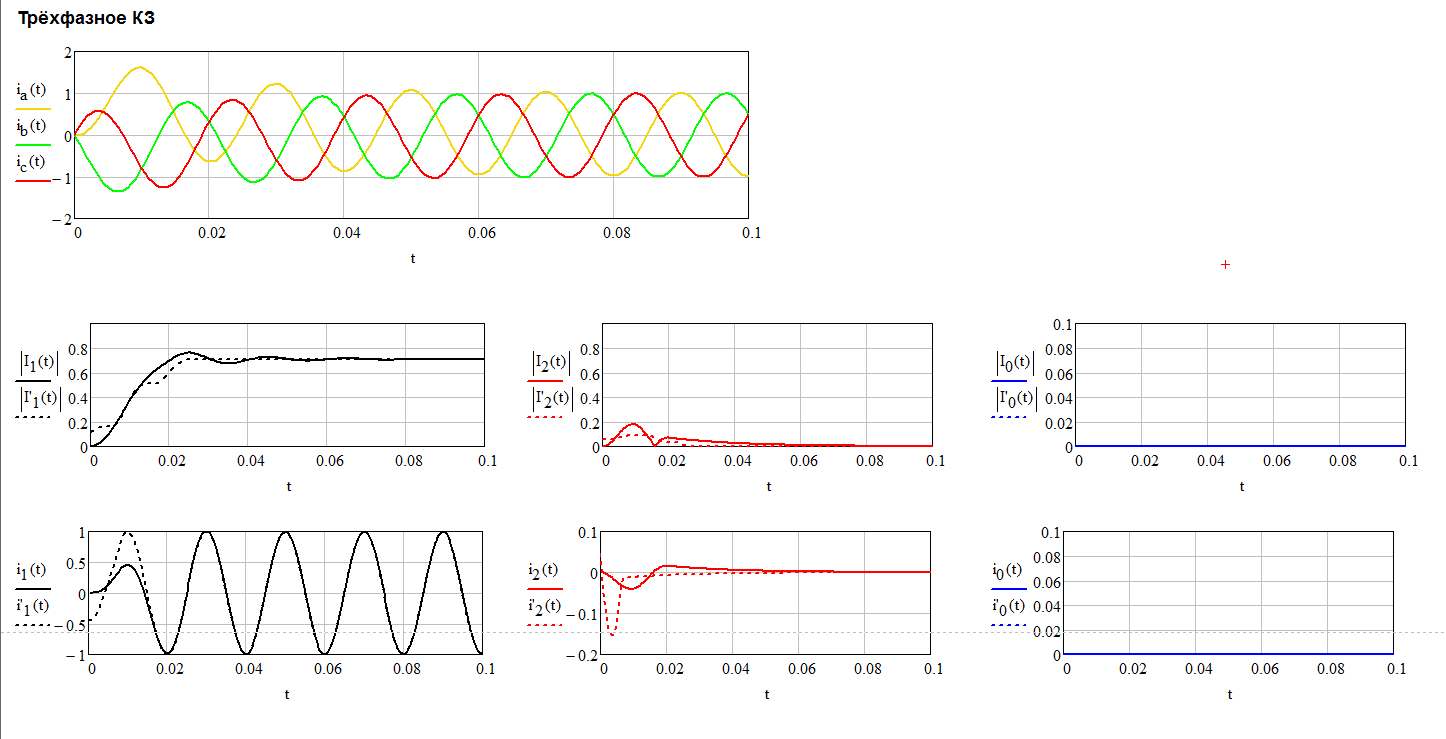
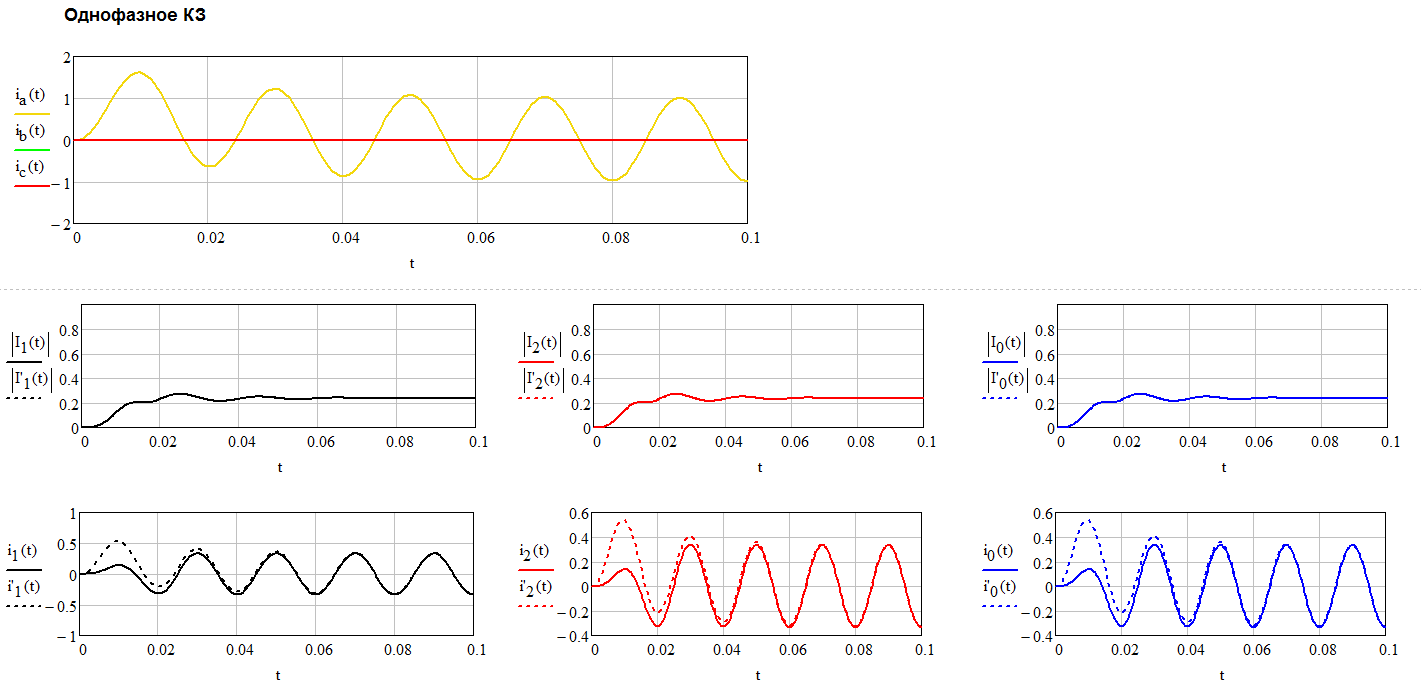
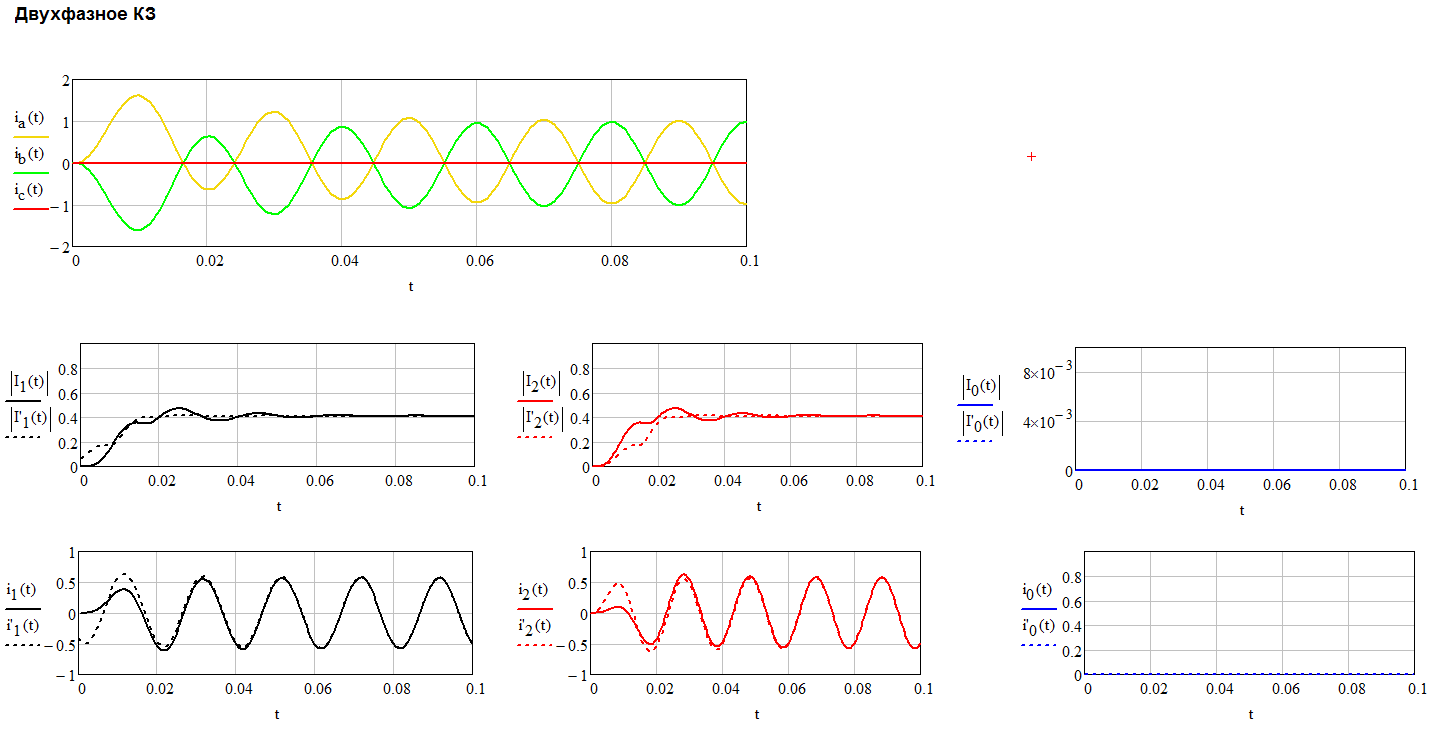
Да, если рассматривать три любых значения на бесконечно малом промежутке времени, на котором величины ua, ub, uc - "не успевают" измениться,
Ну вот, Вы опять по своему пытаетесь объясняете известные всем представления - соответствие изменение и/или текущее положение сигнала во временной плоскости - i = f(t) и текущему положению этой точки в комплексной плоскости - i = Re + jIm (и наоборот), т.е. собственно понятие от куда берётся вектор