Re: Ток небаланса в ДЗТ
Да все это - брехня. Покажите конкретные результаты испытаний, тогда можно и о конкректных результатах говорить.
|
Форум посвящен вопросам релейной защиты и автоматики (РЗА). Обмену опытом и общению релейщиков. |
Вы не вошли. Пожалуйста, войдите или зарегистрируйтесь.
Советы бывалого релейщика → Спрашивайте - отвечаем → Ток небаланса в ДЗТ

|
 |
Да все это - брехня. Покажите конкретные результаты испытаний, тогда можно и о конкректных результатах говорить.
А в случае МП защит - задаются базисные токи. Они тоже задаются с определённой дискретностью. Вот и все выравнивание dfвыр.
Эта погрешность от невозможности точного подбора Ктт, например, с ВН и НН силового Тр от того, что у самого силового Тр Кт нерациональное число, например 35/110 = 0,3181818181818.
Спасибо. Тогда считаю можно эту величину в современных цифровых терминалах не учитывать. Она много меньше всех других погрешностей.
#37,
Противоречий не вижу. Задачи решались разные. Вы находили max(Фурье(exp)), я находил max(Фурье(exp + sin)) = max(Фурье(exp) + Фурье(sin)). Функция максимума нелинейная и дальнейшее упрощение невозможно. И эти максимальные значения могут быть в любом соотношении между друг другом.
Мне кажется, используя формулы в первом сообщении, не надо забывавть что это лишь начальное значение тормозной характеристики. То есть это небаланс дифзащиты в нормальном нагрузочном режиме работы первичного оборудования. Нет там никаких токов КЗ и апериодик больших. Поэтому и расчет ведется в предположении синусоидальных сигналов и сдвига в 90 градусов между током намагничивания и током в нагрузке. А вот когда токи КЗ появляются и небаланс растет тогда и характеристика торможения уставку загрубляет. А так, что суммировать напрямую, что квадраты под корнем складывать, всё равно в конце будет написано что если получилось меньше 0.2 то ставить 0.2. Ну и зачем было считать?
Iкз = 2 крата чем нем ток КЗ? А апериодика - она ведь зависит от фазы напряжения. Если даже для одной фазы апериодики не будет, в двух других будет.
Да тут на самом деле все так аморфно: погрешность принимается 10% хотя она явно столько не будет (при кратности 1-2 Iном), тот же dfвыр принимается 0,02 - 0,05 хотя, на самом деле он будет значительно меньше, если базисные токи задавать с точностью до тысячных, понятно что методика скорее всего рассчитана на отсутствие апериодики.
Но мне тут хочется разобраться не с числами, а с причиной. Поэтому и статью Энергетик пытаюсь найти.
А так, что суммировать напрямую, что квадраты под корнем складывать, всё равно в конце будет написано что если получилось меньше 0.2 то ставить 0.2.
Согласен, тут нет большой разницы, что так, что этак. Но ведь эта формула используется и при расчете коэффициента торможения. А там уже такой фразы нет.
Добавлено: 2024-06-24 18:51:22
Да все это - брехня. Покажите конкретные результаты испытаний, тогда можно и о конкректных результатах говорить.
Хорошо, если будем проводить испытания - давайте определимся с условиями. Значит я рассматриваю режим с токами порядка одного - двух номинальных токов ТТ (1...2) Iном.
Вы утверждаете, что при таких токах будут дикие составляющие высших гармоник? Предполагаю, что вы имели ввиду режим больших токов КЗ, либо наличия большой остаточной намагниченности. Тогда да - дикие гармоники будут. Но при токах (1...2)Iном их в принципе быть не должно, поскольку есть ГОСТы, в соответствии с которыми изготавливают ТТ. Иначе эти ТТ браковались бы на этапе пусконаладки. Предполагаю, что мы друг друга не поняли.
Добавлено: 2024-06-24 19:03:22
Тогда считаю можно эту величину в современных цифровых терминалах не учитывать. Она много меньше всех других погрешностей
Вообще говоря и в электромеханике она не шибко большая была. Но РУ её все таки учитывали, вопрос зачем? Кроме того в руководящих указаниях все составляющие брались по модулю, хотя ошибка расчета при этом (в случае если |I'нб|+|I''нб|+|I'''нб| > |I'нб+I''нб+I'''нб|) больше чем составляющая небаланса, обусловленная неравенством витков I'''нб. Спрашивается зачем РУ учитывали эту никому "непонятную" составляющую I'''нб (по крайней мере мне пока никто не смог объяснить корректный расчет / вывод этой составляющей, хотя на самом деле там нет ничего сложного)? Предполгаю, что РУ её учитывали, поскольку рассматривали все составляющие влияющие на ток небаланса. Вот и здесь (у АББ) та же история, только дополнительно учли физику процесса. А поскольку причины остались не раскрыты, хотелось бы почитать оригинал. А то чесать языком мы все умеем и я в том числе  :D
:D
Добавлено: 2024-06-24 19:10:50
Кстати, а кто нибудь знает - этот алгоритм практически у какого нибудь производителя РЗ используется?
Я конечно детально его не капал, но на первый взгляд там ведь нет ничего сложного.
Хотел сравнить АЧХ этого алгоритма с АЧХ Фурье, но никак руки не доходят.
Кстати, а кто нибудь знает - этот алгоритм практически у какого нибудь производителя РЗ используется?
Я конечно детально его не капал, но на первый взгляд там ведь нет ничего сложного.
Хотел сравнить АЧХ этого алгоритма с АЧХ Фурье, но никак руки не доходят.
Часто под разными назаваниями скрывается эквивалентная математика. А фразы "мы сделали лучше чем Фурье" означают что "стало либо медленнее либо хуже по частотным свойствам". Поэтому хотелось бы понять что конкретно вы имеете в виду.
А фразы "мы сделали лучше чем Фурье" означают что "стало либо медленнее либо хуже по частотным свойствам"
Во первых я таких фраз не говорил - мне самому интересно этот алгоритм лучше или хуже Фурье, поэтому и хочу АЧХ сравнить (при прочих равных, например при равном окне), Во вторых этот алгоритм подробно описан в книге Шнеерсон Э.М. Цифрофая релейная защита. Правда там есть опечатки, но с пониманием разобраться можно. А в общем подход мне нравится: если Фурье разлагает сигнал на систему ортогональных функций, то алгоритм, использующий КИС приближает сигнал к системе собственных функций оптимальным способом в смысле метода наименьших квадратов (кроме того, чем дольше работает алгоритм КИС, тем большую точность можно получить).
| Присоединяйтесь!!! Мы в социальных сетях и на Ютуб. |
А в общем подход мне нравится: если Фурье разлагает сигнал на систему ортогональных функций, то алгоритм, использующий КИС приближает сигнал к системе собственных функций оптимальным способом в смысле метода наименьших квадратов
А, понятно. Ну тут всё зависит от выбранной системы функций. Если будете приближать через МНК суммы синусов/косинусов кратных частот то получите в точности фильтр Фурье. Если добавить экспоненту, то съедут нули АЧХ на кратных частотах и чтобы отдельно подавить высшие гармоники, каждую из них нужно будет добавлять в модель. Это из за того что экспонента не ортогональна синусу/косинусу.
Спасибо. Тогда считаю можно эту величину в современных цифровых терминалах не учитывать. Она много меньше всех других погрешностей.
в РЗ на электромеханике были проблемы с подбором, т.к. ещё нужно было учесть соединение треугольника силового Тр, т.е. \/3 - 1,73 ..., однако и там не было много, например в РНТ и ДЗТ всё можно было поставить с точностью до 1 витка, а у МП этот смещение вектора тока по фазе и величине учитывается без погрешности путём вычисления... и кроме того, правда не везде можно выравнять значения на вторичных преобразователях
Прикол в чём, проверяю курсовые у студентов, они иногда бездумно используют фирменные методички расчёта уставок и её вставляют в расчёт...,
Так вот, практически во всех методах расчёта уставок эта составляющая в расчёте Iнб приведена или участвуется ...
Если добавить экспоненту, то съедут нули АЧХ на кратных частотах
А здесь поподробнее можете пояснить куда они съедут и почему?
А здесь поподробнее можете пояснить куда они съедут и почему?
Первым делом попробуем описать наши данные моделью (первая гармоника известной частоты плюс константа):
a*cos(wt) + b*sin(wt) + C
Предположим у нас на входе есть вектор-столбец y в котором лежит 20 отсчетов входного сигнала. Частота дискретизации 1000 Гц (20 отсчетов на период 50 Гц).
Пусть cos_base вектор-столбец с одним периодом косинуса единичной амплитуды, sin _base - понятно, ones _base вектор столбец из 20-ти единичек.
Напишем 20 уравнений в которых каждую точку сигнала попробуем описать нашей моделью:
a*cos_base + b*sin _base + C*ones _base = y
Или совсем кратко в матричной записи
Ax=y, где матрица А это прямоугольная матрица из трех столбцов [cos_base sin _base ones _base], x = [a b C]' - вектор столбец неизвестных (парамтеров модели).
Решение этой переопределенной СЛАУ и есть задача подкручивания параметров модели a, b, C так чтобы квадрат невязки стал минимальным. Решение МНК эквивалентно умножению исходной системы слева на A' (транспонированная матрица А). Это сделает из переопределенной СЛАУ СЛАУ с квадратной матрицей.
A'*A*x = A'*y
Рассмотрим подробнее A'*A. Это матрица 3x3. На главной диагонали скалярные произведения одноименных вектор-столбцов нашего базиса. Например на месте (1, 1) стоит умножение строки на столбец cos_base' * cos_base = n/2 = 10 (сумма квадратов периода косинуса). На месте (2, 2) стоит тоже самое но для синуса и далее на (3, 3) просто сумма квадратов 20-ти единичек.
А вот во всех остальных местах этой матрицы стоят нули! Потому что вектор-столбцы нашей модели ортогональны друг другу и их скалярное произведение равно нулю. То есть наша матрица это:
10 0 0
0 10 0
0 0 20
Матрица диагональна и это очень хорошо. По сути это означает что у нас тут записано не СЛАУ из трех уравнений а три независимых друг от друга уравнения.
Получается первое уравнение
10*a = cos_base' * y
a = 1/10 * cos_base' * y
Получается что величина косинусной сотавляющей в нашей модели равна коэффициент умножить на сумму произвдений входных данных с периодом косинуса. Так что мы получили фильтр Фурье.
20*C = ones _base' * y
C = 1/20 * ones _base' * y - постоянная составляющая равна сумме входного сигнала за период делить на количество точек, что тоже нас не удивляет.
Почему фильтр Фурье давит все кратные гармоники?
Потому что если в входных данных y будет например синусоида 5-ой гармоники то при скалярном произведении с коэффициентами фильтра (периодом основной гармоники) получится ноль. А ноль получится потому что все косинусы/синусы кратных частот ортогональны друг другу. Они составляют ортогональный базис нашего пространства. И поэтому нет никакой разницы сколько гармоник вводить изначально в модель. Матрица будет всегда диагональной. Если мы посчитали 1-ую гармонику, а потом захотели посчитать еще и 5-ую то мы можем это сделать независимо друг от друга. Это всё плюсы ортогональности базисных функций.
Теперь усложним модель и вместо константы будем пытаться подстроить под данные первую гармонику плюс затухающую экспоненту. Будем использовать вектор столбец exp_base.
Рассмотрим теперь A'*A. Базисные косинус и синус по прежнему ортогональны между собой, а вот скалярное произведение с экспонентой уже не дает ноль. Матрица будет выглядеть как то так
10 0 a13
0 10 a23
a13 a23 a33
Уравнения теперь нельзя решить независимо, только вместе как единую СЛАУ. Предоложим что мы смогли найти обратную матрицу тогда получаем
A'*A*x = A'*y
x = inv(A'*A)*A'*y
Давайте сначала вычислим inv(A'*A)*A' а уж потом будем умножать на вектор столбец данных.
Здесь мы имеем квадратную (не диагональную) матрицу inv(A'*A) размерности 3х3, которая умножается на матрицу состоящую из трех строк. В первой строке cos_base', во второй sin_base' в третьей exp_base'.
Результатом будет прямоугольная матрица в которой в каждой строке будет линейная комбинация всех первоначальных строк с какими то коэффициентами.
Это и есть ответ. Чтобы найти косинусную составляющую в такой модели необходимо данные y умножить на коэффициенты фильтра, которые являются линейной комбинацией базисного косинуса, синуса и экспоненты. Можно построить АЧХ и посмотреть на нее.
Но так как в коэффициентах есть какая то часть от exp_base' то умножение на чистые синусоиды кратных частот (которые могут быть в данных y) уже никогда не дадут нуля так как эти функции (вектор-столбцы кратной гармоники и экспоненты) не ортогональны. А это значит что данный фильтр уже не давит кратные частоты. Ни одну. Более того так как матрица не диаогнальная то мы не можем не пересчитывая первую гармонику взять и посчитать пятую. Для каждого набора базисных функций свои конечные коэффициенты.
Предположим у нас на входе есть вектор-столбец y в котором лежит 20 отсчетов входного сигнала.
Насколько я понял вы рассматриваете абстрактный вектор столбец y, который я пока не понял из чего он у вас состоит, насколько понял может быть любым. В этом случае да, погрешность будет и даже в том случае, когда базисный вектор экспоненты заменен единичным вектором (т.е. если мы приближаем сигнал системой трех функций 1, cos, sin). Её не будет только в том случае если исходный сигнал уже лежит в пространстве функций 1, cos, sin (это должно быть вроде как очевидно, и тут даже не должно смущать, что мы работаем в пространстве 20 измерений (20 отсчетов за период), а базисных функций у нас только 3, ведь исходный сигнал все равно будет лежать в системе базисных функций, тогда понятно, что и погрешности быть не должно). Тоже и с системой e, cos, sin. Если исходный сигнал лежит в пространстве этих функций то погрешности не будет, если не лежит, то будет.
Кстати вот сравнение работы фильтра Фурье и фильтра КИС (выделяется первая гармоника) в случае, если входной сигнал представлен только синусоидальной функцией и экспонентой затухающей с постоянной 1 сек. (Алгоритм КИС выполним так, чтобы он приближал входной сигнал системой функций e, cos, sin)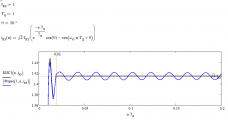 https://rzia.ru/uploads/images/8952/04c0e115d2d2a0704b3265aa0705014c.png
https://rzia.ru/uploads/images/8952/04c0e115d2d2a0704b3265aa0705014c.png
Из графика видно, что как у фильтра Фурье, так и фильтра КИС есть инерционность, но после интервала у фильтра КИС погрешности нет, а фильтра Фурье погрешность есть.
А вот, что будет если входной сигнал представить через сумму синусоидальной функции и некой абстрактной постоянной величины (а Алгоритм КИС оставить прежним, т.е. таким, чтобы он приближал входной сигнал системой функций e, cos, sin):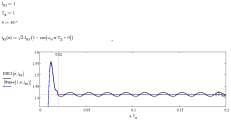 https://rzia.ru/uploads/images/8952/fabc2a39d21561fee1a1bd55e6fe7c9f.png
https://rzia.ru/uploads/images/8952/fabc2a39d21561fee1a1bd55e6fe7c9f.png
Тут уже наоборот Фурье работает без погрешности, а КИС с погрешностью (как раз потому, что входной сигнал не лежит в пространстве функций e, cos, sin)
Таким образом получается, что чем больше собственных функций учесть в алгоритме КИС тем будет лучше, но всё учесть наверное невозможно, поэтому этот алгоритм используется не повсеместно. И все же Шнеерсон писал, что где то он все таки применялся (ссылаясь на статью Sashdev M.S. A new algorithm for digital ... но я её не нашел). Интересно было бы почитать.
Добавлено: 2024-06-26 13:24:39
Кстати эта инерционность также объясняется тем, что фильтр КИС с окном 20 отсчетов берет отсчеты до возникновения КЗ. Следовательно на интервале первых 20 отсчетов входной сигнал в принципе не будет лежать в пространстве базисных функций фильтра КИС, поэтому и видим дикие колебания.
Добавлено: 2024-06-26 13:29:24
и тут даже не должно смущать, что мы работаем в пространстве 20 измерений (20 отсчетов за период), а базисных функций у нас только 3
Кстати вообще говоря из этого следует, что в этом случае нам достаточно 3 измерений вместо 20. А это уже интересно))
Её не будет только в том случае если исходный сигнал уже лежит в пространстве функций 1, cos, sin (это должно быть вроде как очевидно, и тут даже не должно смущать, что мы работаем в пространстве 20 измерений (20 отсчетов за период), а базисных функций у нас только 3, ведь исходный сигнал все равно будет лежать в системе базисных функций, тогда понятно, что и погрешности быть не должно).
Не совсем. Если базисные функции будут 1, cos, sin а сигнал будет первая гармоника плюс третья гармоника то формально сигнал не лежит в базисе, тем не менее это никак не влияет на определение составляющих вдоль базиса. Они будут получены без погрешностей.
А вот если базис это e, sin, cos то без погрешности будет считаться только сигнал линейная комбинация базисных. Добавление в сигнал третьей гармоники испортит все расчеты. Проблема в неортогональности базиса.
Таким образом получается, что чем больше собственных функций учесть в алгоритме КИС тем будет лучше, но всё учесть наверное невозможно, поэтому этот алгоритм используется не повсеместно. И все же Шнеерсон писал, что где то он все таки применялся (ссылаясь на статью Sashdev M.S. A new algorithm for digital ... но я её не нашел).
Если точек в векторе 20 то и базисных функций 20. Для фурье это 1, sin и сos с 1-ой по 9-ую гармоники и отдельно 10 гармоника которая просто чередующиеся плюс один, минус один. Так как базис ортогональный можно находить каждую составляющую независимо по простому выражению. А можно выкинуть 1 и взять e. Но придется решить СЛАУ из 10 уравнений.
Статья ищется на sci-hub без проблем.
Так же стоит отметить что экспоненты имеют разные постоянные времени, а во всех выражениях выше имеется в виду что она заранее известна.
Кстати вообще говоря из этого следует, что в этом случае нам достаточно 3 измерений вместо 20. А это уже интересно))
В реальности работать нормально не будет (при 20 точках на период). АЧХ будет ужасная, подавления шумов никакого.
Так же стоит отметить что экспоненты имеют разные постоянные времени, а во всех выражениях выше имеется в виду что она заранее известна.
Так вы сами рассматривали простую экспоненту, поэтому я и взял Та = 1. А вообще её надо раскладывать в ряд Тейлора.
Если базисные функции будут 1, cos, sin а сигнал будет первая гармоника плюс третья гармоника то формально сигнал не лежит в базисе, тем не менее это никак не влияет на определение составляющих вдоль базиса.
Давайте проверим. При наличии 3й гармоники в исходном сигнале первая гармоника уже будет определяться с погрешностью.
Вы ведь представляете как работает операция (Аt*А)^-1*Аt*b: ведь А - это по сути и есть совокупность векторов (в нашем случае базисных функций) на которые проецируется вектор b (в нашем случае это входной сигнал iкз). Если b лежит в пространстве векторов А, то решение будет соответствовать случаю А^-1*b. А как входной сигнал с 3й гармоникой может лежать в пространстве 1, cos, sin, если cos и sin - это только первая гармоника. Вот если бы базисные функции состояли из 1, cos, sin, cos3, sin3, то другое дело.
Вот что будет если есть 3я гармоника и мы используем систему e, cos, sin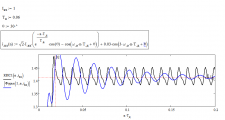 https://rzia.ru/uploads/images/8952/b1564f8120de9b3a8554aca765cb0806.png
https://rzia.ru/uploads/images/8952/b1564f8120de9b3a8554aca765cb0806.png
А вот что будет если мы будем использовать систему e, cos, sin, cos3, sin3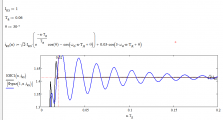 https://rzia.ru/uploads/images/8952/93b8c3bd0e29e88f3bdeeab8ddcca088.png
https://rzia.ru/uploads/images/8952/93b8c3bd0e29e88f3bdeeab8ddcca088.png
Добавлено: 2024-06-26 17:28:31
Это для Фурье 20 функций, а для КИС столько функций сколько заложено или вы под cos и sin имели ввиду все гармоники с 1-ой по 9-ую? Я имел ввиду только 1-ую (ну это для КИС)
Добавлено: 2024-06-26 17:29:44
Ссылочку можете скинуть? У меня говорит этого документа нет в базе.
А как входной сигнал с 3й гармоникой может лежать в пространстве 1, cos, sin, если cos и sin - это только первая гармоника. Вот если бы базисные функции состояли из 1, cos, sin, cos3, sin3, то другое дело.
так он и не лежит. Но их наличие не меняет величин проекций на 1, cos, sin в силу ортогональности. Вы посчитатйте разложение в базисе 1, cos, sin у сигнала например cos + cos3. Будет тоже самое что и просто у cos. Мы вроде говорим об одном а в итоге вы раскладываете на e, cos, sin
А вот что будет если мы будем использовать систему e, cos, sin, cos3, sin3
Вот в том то и дело что как только вместо 1 появляется e нам нужно брать все базисные функции чтобы решить СЛАУ совместно. А когда была "1" можно было находить составляющие независимо.
Это для Фурье 20 функций, а для КИС столько функций сколько заложено или вы под cos и sin имели ввиду все гармоники с 1-ой по 9-ую? Я имел ввиду только 1-ую (ну это для КИС)
Да я тоже имел в виду под cos, sin только первую гармонику. Это было к тому что в КИС максимально можно заложить функций по количеству совпадающую с размерностью пространства.
Мы вроде говорим об одном а в итоге вы раскладываете на e, cos, sin
ну случай 1, cos, sin - он как раз даст Фурье, а мне надо было показать отличие (я как раз хотел показать, что фильтром КИС можно подавить апериодику почти в ноль). Тем более, что случай 1, cos, sin не подходит к структуре сигналов ЭЭС. Т.е. функции 1 как правило в реальном сигнале нет, а вот функция exp есть. Я видимо просто вас не понял.
Добавлено: 2024-06-26 19:02:34
Большое спасибо за ссылку
Добавлено: 2024-06-26 19:09:31
Вот в том то и дело что как только вместо 1 появляется e нам нужно брать все базисные функции чтобы решить СЛАУ совместно. А когда была "1" можно было находить составляющие независимо.
В этом собственно и будет преимущество алгоритма КИС перед Фурье. Поскольку Фурье в этом случае будет давать погрешность, а КИС нет
Я как-то давно моделировал китайский алгоритм подавления апериодики.
Апериодику давит в ноль, зато всякие ВЧ махры и еще какая-то мелочь, на выходе амплитуда немного похожая на пилу, мотает туда-сюда, может процентов 10 погрешность, но все равно по-моему давление апериодики в ноль не всегда хороший вариант.
кстати если N < 20, то Фурье придется допиливать, а КИС нет, поскольку эти функции уже не будут ортоганальны на этом интервале.
Добавлено: 2024-06-28 17:06:40
Хотел сравнить АЧХ этого алгоритма с АЧХ Фурье, но никак руки не доходят.
Вот построил. В качестве базисных функций взял e (разложенную в ряд Тейлора, ограничился 3 членами) и функции cos и sin с 1-ой по 5-ю гармоники.
Там на больших частотах получилось, что фильтр КИС начинает усиливать сигнал, поэтому привел графики в логарифмическом масштабе. в общем вот такие результаты: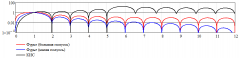 https://rzia.ru/uploads/images/8952/db235431eba472ab441c8e1e0dc9c400.png
https://rzia.ru/uploads/images/8952/db235431eba472ab441c8e1e0dc9c400.png
Понятно теперь почему в этом алгоритме ФНЧ нужен. Без него никуда.
кстати если N < 20, то Фурье придется допиливать, а КИС нет, поскольку эти функции уже не будут ортоганальны на этом интервале.
Можно просто сказать что Фурье это частный случай КИС с конкретными базисными функциями.
В этом собственно и будет преимущество алгоритма КИС перед Фурье. Поскольку Фурье в этом случае будет давать погрешность, а КИС нет
Но как вы и показали КИС будет усиливать ВЧ составляющую (а значит и шум) и не будет давить кратные гармоники.
Я считаю что гармоники кратные давить надо, так как экспонента только во время коммутаций а высшие гармоники в токах могут быть постоянно (особенно нечетные).
Понятно теперь почему в этом алгоритме ФНЧ нужен. Без него никуда.
А добавите ФНЧ значит сразу возрастет прядок всего тракта и сравнивать с Фурье на периоде вообще уже нельзя будет. Если к Фурье прикрутить еще фильтр то тоже лучше будет.
Тем не менее можно сделать так. Сравнить Фурье и КИС у которого в качестве базисных функций взяты все те же самые как и в Фурье но константа заменена на экспоненту. В этом случае дествительно будет неполохо. Никакого увеличения ВЧ и полное подавление выбранной апериодики. Если определять постоянную времени как то извне и не переживать что на каждом такте расчета придется полностью решать СЛАУ то почему бы и нет. Но по вычислениям будет конечно сильно больше.
А если как вы начать раскладывать экспоненту в ряд Тейлора то придется жертвовать подавлением каких то гармоник чтобы базисных функций осталось 20 (при 20 точках на периоде). И как только мы пожертвуем какой то гармоникой так там сразу АЧХ выпучивается.
Вот кстати статья, которую вы искали
Данный контент доступен только зарегистрированным пользователям.
но все равно по-моему давление апериодики в ноль не всегда хороший вариант
Есть тем не менее удачные алгортимы для решения этой задачи.
Есть тем не менее удачные алгортимы для решения этой задачи.
Есть алгоритм дистанционной защиты (а-ля ЭКРА) с использованием дифференциальных уравнений линии. На самом деле это я так понимаю просто низкочастотный фильтр, т.к. когда находят u=R*i+L*di/dt, то di/dt подавит апериодику, если замерное сопротивление будет с большим L, а если там малое L то апериодики там толком нет.
Может, это кстати самый нормальный вариант, по сути брать ток и напряжение одновременно и смотреть по ним, но его сложно адаптировать для чего-то помимо ДЗ.
Можно просто продифференцировать сигнал, тогда апериодика, которая затухает долго, почти исчезнет, а если она затухает быстро, то ее влияние будет недолгим.
+ видел фильтры, настроенные под какую-то конкретную постоянную времени.
Но честно говоря, не до конца разобрался, как лучше.
В том то и дело, что постоянная затухания нам не известна. Поэтому насколько я понял и раскладывают эту экспоненту в ряд Тейлора (что у Шашдева, что у Шнеерсона).
А вообще да, если бы постоянная затухания нам была бы известна, то получается почти идеальный фильтр Фурье.
А добавите ФНЧ значит сразу возрастет прядок всего тракта и сравнивать с Фурье на периоде вообще уже нельзя будет.
хз иногда вроде ФНЧ в аналоговых входах применяют, по крайней мере раньше ставили или я уже не в трэнде?  :D
:D
За статью большое спасибо, но к сожалению там даже намека нет на нашу формулу. Видимо так и не узнаем почему отсутствие апериодики берётся за расчетный случай. Либо так проще было считать, либо действительно у АББ есть алгоритмы, которые давят апериодику.
Тьфу, опять о том же. Сплошная математика. А физика где же? Может кто-то привести конкретные примеры реального поведения ДЗТ в конкретных условиях работы? Да, с ЭКРА или РА я могу напрямую найти контакты. В меньшей степени - ЧЭАЗ. Но все же больше интересует мнение конечного потребителя.
Советы бывалого релейщика → Спрашивайте - отвечаем → Ток небаланса в ДЗТ
Форум работает на PunBB, при поддержке Informer Technologies, Inc
